kumpulan referensi: Spherical cap

Sabtu, 06 Agustus 2011

Spherical cap

From Wikipedia, the free encyclopedia

The spherical cap is the purple section.

In geometry, a spherical cap is a portion of a sphere cut off by a plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere.

If the radius of the sphere is

r

, the radius of the base of the cap is

a

, and the height of the cap is

h

, then the volume of the spherical cap is

$V = \frac{\pi h}{6} (3a^2 + h^2),$

and the curved surface area of the spherical cap is

A = 2π r h .

The parameters

a

h

and

r

are not independent:

r 2 = (r - h) 2 + a 2 = r 2 + h 2 - 2 r h + a 2,

$r = \frac {a^2 + h^2}{2h}$ .

Substituting this into the area formula gives:

$A = 2 \pi \frac{(a^2 + h^2)}{2h} h = \pi (a^2 + h^2).$

Note also that in the upper hemisphere of the diagram, $\scriptstyle h = r - \sqrt{r^2 - a^2}$ , and in the lower hemisphere $\scriptstyle h = r + \sqrt{r^2 - a^2}$ ; hence in either hemisphere $\scriptstyle a = \sqrt{h(2r-h)}$ and so an alternative expression for the volume is

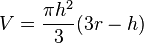$V = \frac {\pi h^2}{3} (3r-h)$ .

kumpulan referensi

Sabtu, 06 Agustus 2011

Spherical cap

Spherical cap

Tidak ada komentar:

Posting Komentar

Pengikut